LEETCODE 股票买卖问题

穷举

动态规划的本质就是穷举「状态」，在「选择」中选择最优解。

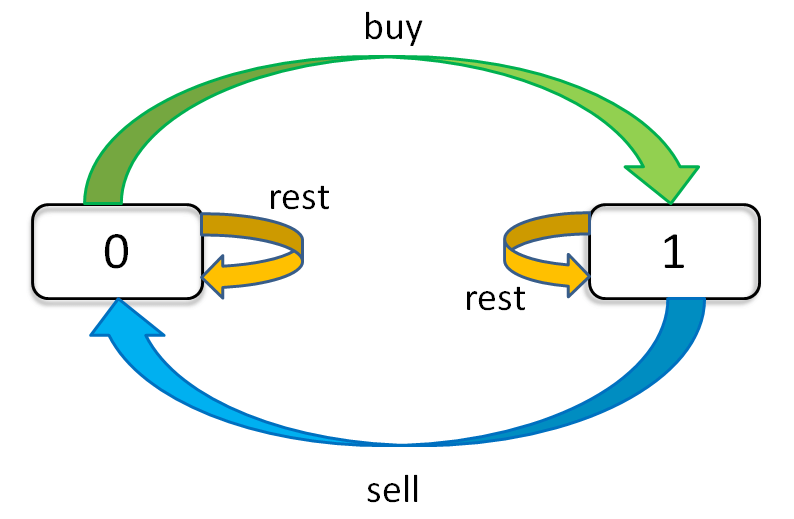
那么对应题目，每天的状态就是 buy购买、sell卖出、rest无操作。

另外，buy后才能sell，sell后才能buy，rest也分为 buy后和 sell后，而且我们还需要考虑交易次数k的限制，buy时k>0。

这个问题的状态有三个，用一个dp三维数组表示，第一个是天数，第二个是允许交易最大次数，第三个是当前是否持有（用0，1来表示）。

那么答案就是dp[n - 1][k][0]，即最后一天，最多允许交易k次，最多获得的利润。

状态转移

完成了穷举，我们就要开始思考面临的选择有哪些，如何更新状态。

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max( 今天选择 rest,        今天选择 sell       )

解释：今天我没有持有股票，有两种可能，我从这两种可能中求最大利润：

1、我昨天就没有持有，且截至昨天最大交易次数限制为 k；然后我今天选择 rest，所以我今天还是没有持有，最大交易次数限制依然为 k。

2、我昨天持有股票，且截至昨天最大交易次数限制为 k；但是今天我 sell 了，所以我今天没有持有股票了，最大交易次数限制依然为 k。

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max( 今天选择 rest,         今天选择 buy         )

解释：今天我持有着股票，最大交易次数限制为 k，那么对于昨天来说，有两种可能，我从这两种可能中求最大利润：

1、我昨天就持有着股票，且截至昨天最大交易次数限制为 k；然后今天选择 rest，所以我今天还持有着股票，最大交易次数限制依然为 k。

2、我昨天本没有持有，且截至昨天最大交易次数限制为 k - 1；但今天我选择 buy，所以今天我就持有股票了，最大交易次数限制为 k。

这里着重提醒一下，时刻牢记「状态」的定义，状态 k 的定义并不是「已进行的交易次数」，而是「最大交易次数的上限限制」。如果确定今天进行一次交易，且要保证截至今天最大交易次数上限为 k，那么昨天的最大交易次数上限必须是 k - 1。

这个解释应该很清楚了，如果 buy，就要从利润中减去 prices[i]，如果 sell，就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。

注意 k 的限制，在选择 buy 的时候相当于开启了一次交易，那么对于昨天来说，交易次数的上限 k 应该减小 1。

base case

定义 base case，即最简单的情况。

dp[-1][...][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0。

dp[-1][...][1] = -infinity
解释：还没开始的时候，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。

dp[...][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0。

dp[...][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。

题解

class Solution {
    public int maxProfit(int max_k, int[] prices) {
        int n = prices.length;
        if (n <= 0) {
            return 0;
        }
        if (max_k > n / 2) {
            // 交易次数 k 没有限制的情况
            return maxProfit_k_inf(prices);
        }

        // base case：
        // dp[-1][...][0] = dp[...][0][0] = 0
        // dp[-1][...][1] = dp[...][0][1] = -infinity
        int[][][] dp = new int[n][max_k + 1][2];
        // k = 0 时的 base case
        for (int i = 0; i < n; i++) {
            dp[i][0][1] = Integer.MIN_VALUE;
            dp[i][0][0] = 0;
        }

        for (int i = 0; i < n; i++)
            for (int k = max_k; k >= 1; k--) {
                if (i - 1 == -1) {
                    // 处理 i = -1 时的 base case
                    dp[i][k][0] = 0;
                    dp[i][k][1] = -prices[i];
                    continue;
                }
                // 状态转移方程
                dp[i][k][0] = Math.max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]);
                dp[i][k][1] = Math.max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);
            }
        return dp[n - 1][max_k][0];
    }

    // 第 122 题，k 无限的解法
    private int maxProfit_k_inf(int[] prices) {
        int n = prices.length;
        int[][] dp = new int[n][2];
        for (int i = 0; i < n; i++) {
            if (i - 1 == -1) {
                // base case
                dp[i][0] = 0;
                dp[i][1] = -prices[i];
                continue;
            }
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[n - 1][0];
    }
}
// 详细解析参见：
// https://labuladong.github.io/article/?qno=188

LEETCODE 股票买卖问题 #

穷举 #

状态转移 #

base case #

题解 #

LEETCODE 股票买卖问题

穷举

状态转移

base case

题解