并查集算法 #

主要是解决图论中「动态连通性」问题。

动态连通性其实可以抽象成给一幅图连线。比如下面这幅图，总共有 10 个节点，他们互不相连，分别用 0~9 标记：

Union-Find 算法主要需要实现这两个 API：

class UF {
    /* 将 p 和 q 连接 */
    public void union(int p, int q);
    /* 判断 p 和 q 是否连通 */
    public boolean connected(int p, int q);
    /* 返回图中有多少个连通分量 */
    public int count();

这里所说的「连通」是一种等价关系，也就是说具有如下三个性质：

1、自反性：节点 p 和 p 是连通的。

2、对称性：如果节点 p 和 q 连通，那么 q 和 p 也连通。

3、传递性：如果节点 p 和 q 连通，q 和 r 连通，那么 p 和 r 也连通。

比如说之前那幅图，0～9 任意两个不同的点都不连通，调用 connected 都会返回 false，连通分量为 10 个。

如果现在调用 union(0, 1)，那么 0 和 1 被连通，连通分量降为 9 个。

再调用 union(1, 2)，这时 0,1,2 都被连通，调用 connected(0, 2) 也会返回 true，连通分量变为 8 个。

算法实现 #

使用每个节点用一棵树来表示图的动态连通性，用数组来具体实现这个森林。

怎么表示结点的连通性？ #

我们设定每个节点有一个指针指向其父结点，如果是根节点的话，这个指针指向自己。

算法优化 #

平衡性优化 #

一开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面，那么这里就可能出现「头重脚轻」的不平衡状况。

我们希望，小一些的树接到大一些的树下面，这样就能避免头重脚轻，更平衡一些。解决方法是额外使用一个 size 数组，记录每棵树包含的节点数。

这样，通过比较树的重量，就可以保证树的生长相对平衡，树的高度大致在 logN 这个数量级，极大提升执行效率。

路径压缩 #

其实我们并不在乎每棵树的结构长什么样，只在乎根节点。如果我们能够压缩树的高度，是树高始终保持为常树。

路径压缩的效果如下:

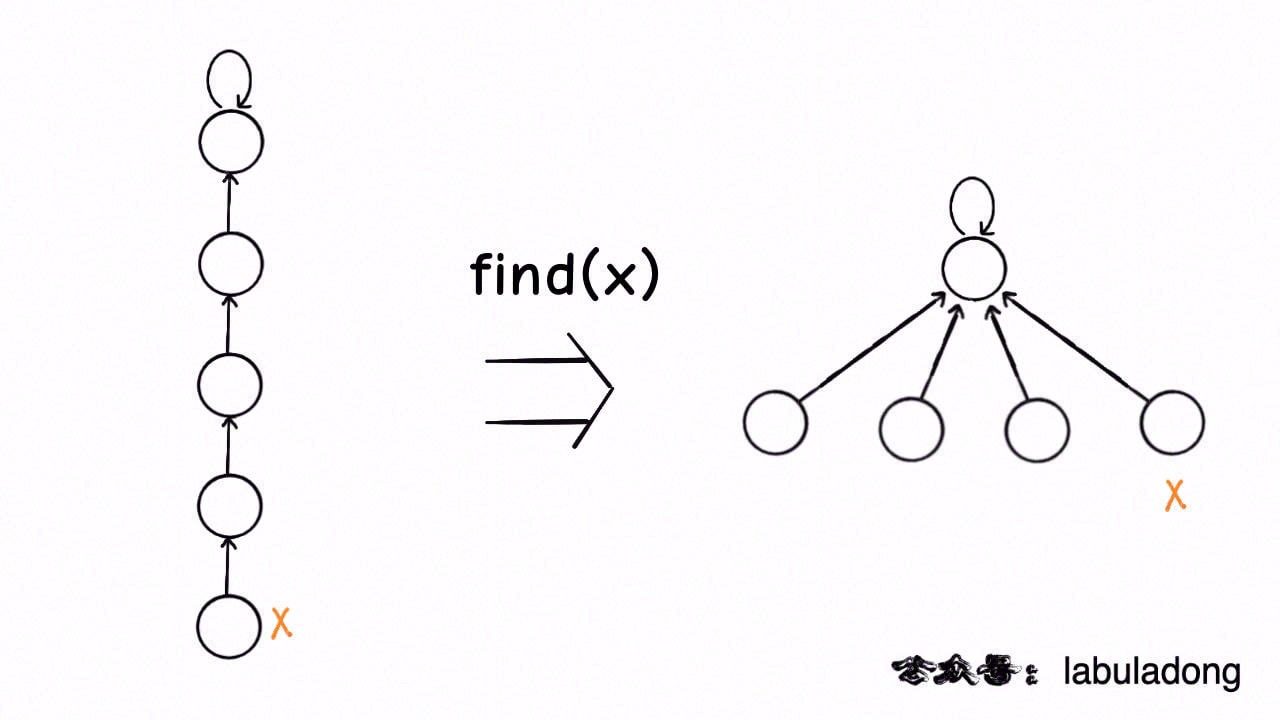另外，如果路径压缩技巧将树高保持为常数了，那么 size 数组的平衡优化就不是特别必要了。

完整的算法代码：