拓扑排序详解及运用 #

环检测算法（DFS 版本） #

什么时候无法修完所有课程？当存在循环依赖的时候。其实这种场景在现实生活中也十分常见，比如我们写代码 import 包也是一个例子，必须合理设计代码目录结构，否则会出现循环依赖，编译器会报错，所以编译器实际上也使用了类似算法来判断你的代码是否能够成功编译。

看到依赖问题，首先想到的就是把问题转化成「有向图」这种数据结构，只要图中存在环，那就说明存在循环依赖。

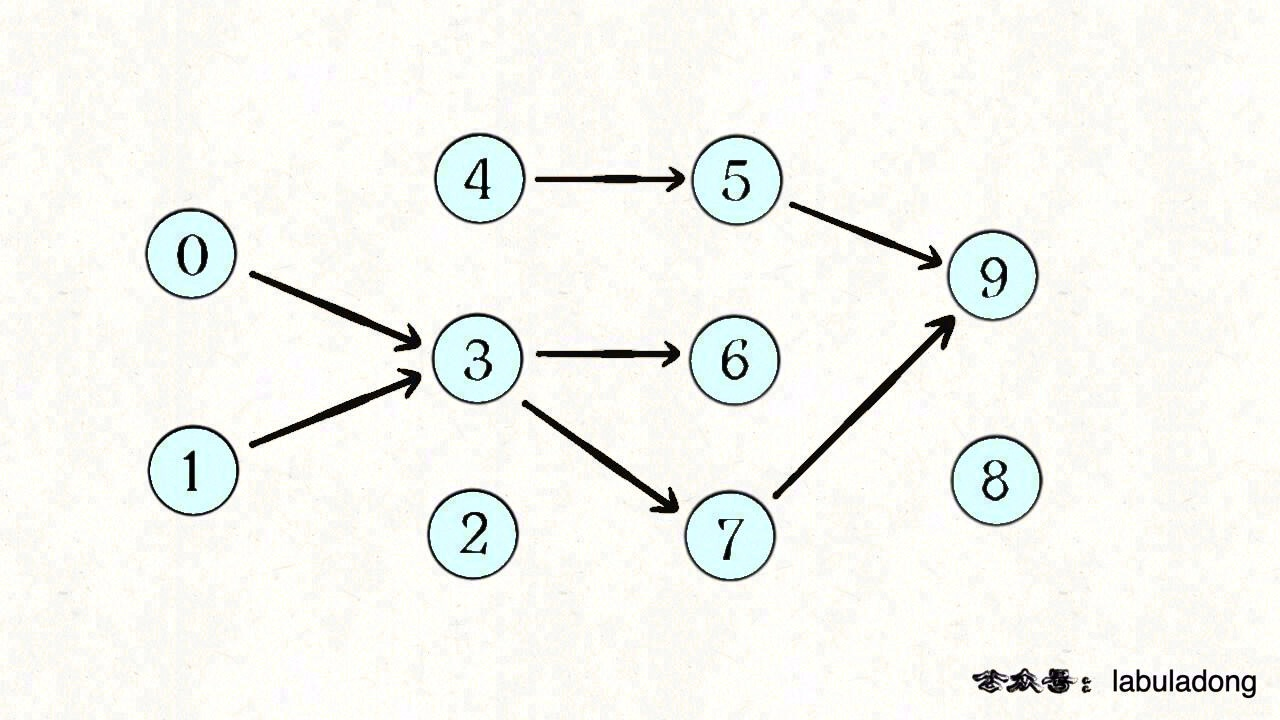
首先我们要把题目的输入转化成一幅有向图，然后再判断图中是否存在环。常见的我们使用邻接表来表述。

graph[s] 是一个列表，存储着节点 s 所指向的节点。我们先建一下图。

接着套用DFS遍历模板，在此基础上新增两个辅助数组: visited 标记访问过的项，onPath 标记遍历过程中路径上的项，和一个辅助变量：hasCycle 表示是否存在环。

上述 GIF 描述了递归遍历二叉树的过程，在 visited 中被标记为 true 的节点用灰色表示，在 onPath 中被标记为 true 的节点用绿色表示。

在遍历图的过程中顺便判断是否存在环，完整代码如下：

拓扑排序 #

什么是拓扑排序 #

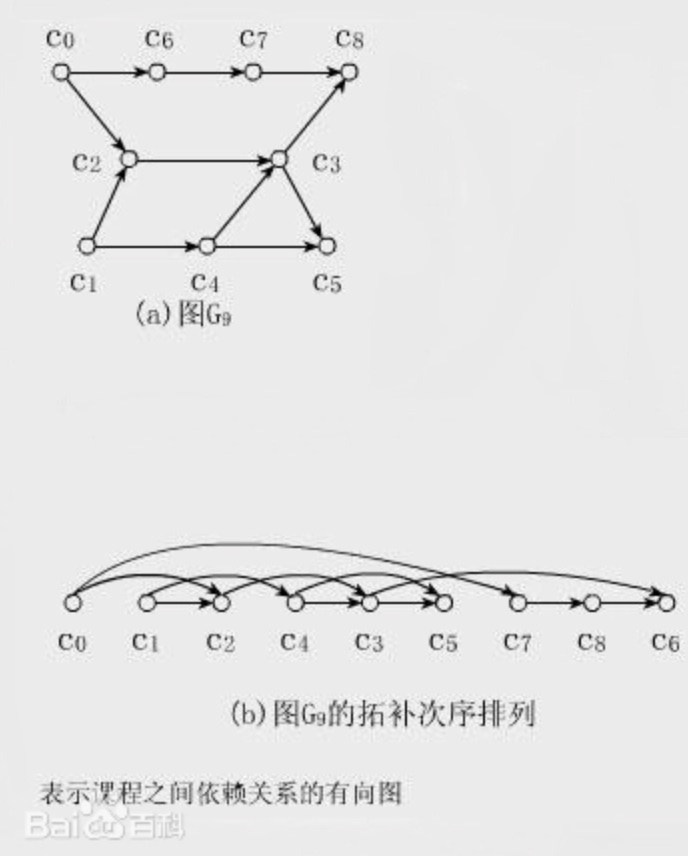
直观地说就是，让你把一幅图「拉平」，而且这个「拉平」的图里面，所有箭头方向都是一致的，比如上图所有箭头都是朝右的。

很显然，如果一幅有向图中存在环，是无法进行拓扑排序的，因为肯定做不到所有箭头方向一致；反过来，如果一幅图是「有向无环图」，那么一定可以进行拓扑排序。

但是我们这道题和拓扑排序有什么关系呢？

其实也不难看出来，如果把课程抽象成节点，课程之间的依赖关系抽象成有向边，那么这幅图的拓扑排序结果就是上课顺序。

首先，我们先判断一下题目输入的课程依赖是否成环，成环的话是无法进行拓扑排序的。

同时在遍历过程中，生成后续遍历结果，而后续遍历反转的结果，则是拓扑排序的结果。

(也可以把to和from交换一下位置，即可不用反转)