算法性能分析 #

时间复杂度分析 #

什么是时间复杂度 #

时间复杂度是一个函数，用来描述算法的运行时间。

假设算法的问题规模为n，那么程序运行的操作次数我们用一个函数f(n)来表示，随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，这就称为时间复杂度，记为O(f(n))。

而O是用来表示上界的，一个最坏情况时间的上界。

但严格从大O的定义来讲，快速排序的时间复杂度应该是O(n^2)。但是我们依然说快速排序是O(nlogn)的时间复杂度，这个就是业内的一个默认规定，这里说的O代表的就是一般情况，而不是严格的上界。

面试中说道算法的时间复杂度是多少指的都是一般情况。但是如果面试官和我们深入探讨一个算法的实现以及性能的时候，就要时刻想着数据用例的不一样，时间复杂度也是不同的，这一点是一定要注意的

不同数据规模的差异 #

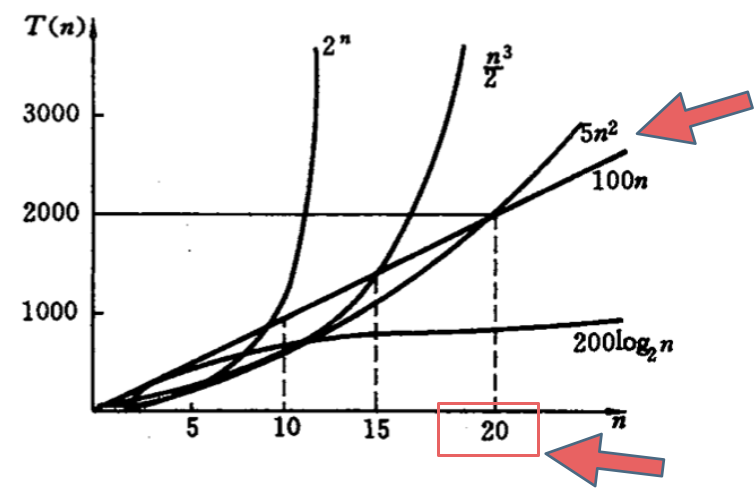在决定使用哪些算法的时候，不是时间复杂越低的越好，要考虑数据规模，如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适（在有常数项的时候）。

就像上图中 O(5n^2) 和 O(100n) 在n为20之前，很明显 O(5n^2)是更优的，所花费的时间也是最少的。

那为什么在计算时间复杂度的时候要忽略常数项系数呢，而且要默认O(n) 优于O(n^2) 呢？

因为大O就是数据量级突破一个点且数据量级非常大的情况下所表现出的时间复杂度，这个数据量也就是常数项系数已经不起决定性作用的数据量。

所以我们说的时间复杂度都是省略常数项系数的，是因为一般情况下都是默认数据规模足够的大，基于这样的事实，给出的算法时间复杂的的一个排行如下所示：

O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n^2)平方阶 < O(n^3)立方阶 < O(2^n)指数阶

但是也要注意大常数，如果这个常数非常大，例如10^7 ，10^9 ，那么常数就是不得不考虑的因素了。

递归算法的时间复杂度 #

递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归中的操作次数。

同样使用递归，可以写出O(logn)的代码，也可以写出O(n)的代码。

计算x的n次方

// 时间复杂度O(n)
int function1(int x, int n) {
    int result = 1;  // 注意 任何数的0次方等于1
    for (int i = 0; i < n; i++) {
        result = result * x;
    }
    return result;
}
// 时间复杂度O(n)
int function3(int x, int n) {
    if (n == 0) {
        return 1;
    }
    if (n % 2 == 1) {
	    // 此处重复计算了
        return function3(x, n / 2) * function3(x, n / 2)*x;
    }
    return function3(x, n / 2) * function3(x, n / 2);
}

// 时间复杂度O(logn)
int function4(int x, int n) {
    if (n == 0) {
        return 1;
    }
    int t = function4(x, n / 2);// 这里相对于function3，是把这个递归操作抽取出来
    if (n % 2 == 1) {
        return t * t * x;
    }
    return t * t;
}

空间复杂度分析 #

什么是空间复杂度呢？

是对一个算法在运行过程中占用内存空间大小的量度，记做S(n)=O(f(n))。空间复杂度是考虑程序运行时占用内存的大小，而不是可执行文件的大小。

空间复杂度O(1)

int j = 0;
for (int i = 0; i < n; i++) {
    j++;
}

空间复杂度O(n)

int* a = new int(n);
for (int i = 0; i < n; i++) {
    a[i] = i;
}

在递归的时候，会出现空间复杂度logn的情况。

递归算法的性能分析 #

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

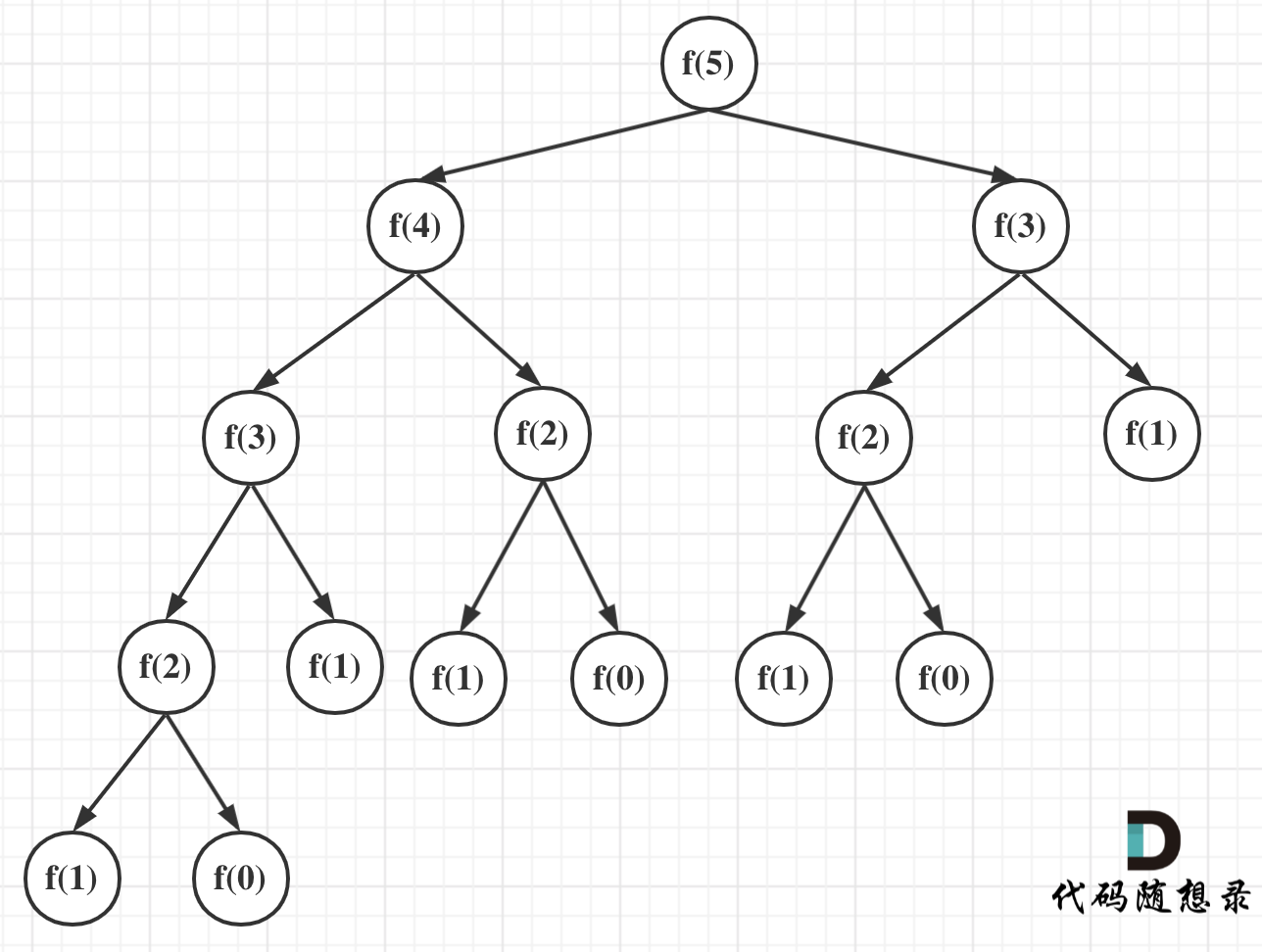
我们可以看到，f(5)是由f(4)和f(3)相加而来，那么f(4)是由f(3)和f(2)相加而来以此类推。

在这课二叉树中每个节点都是一次递归，一棵深度为k的二叉树最多可以有2^k - 1个结点。所以时间复杂度是O(2^n)。

优化一下：

int fibonacci(int first, int second, int n) {
    if (n <= 0) {
        return 0;
    }
    if (n < 3) {
        return 1;
    }
    else if (n == 3) {
        return first + second;
    }
    else {
	    // 这里相当于用first和second来记录当前相加的两个数值，减少了一次递归，时间复杂度是O(n)
        return fibonacci(second, first + second, n - 1);
    }
}

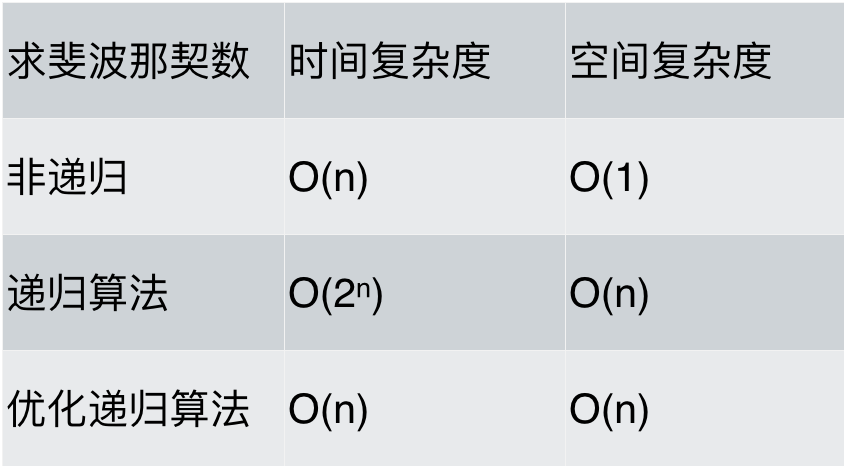
空间复杂度分析 #

递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度

代码的内存消耗 #

不同语言的内存管理 #

不同的编程语言各自的内存管理方式。

• C/C++这种内存堆空间的申请和释放完全靠自己管理
• Java 依赖JVM来做内存管理，不了解jvm内存管理的机制，很可能会因一些错误的代码写法而导致内存泄漏或内存溢出
• Python内存管理是由私有堆空间管理的，所有的python对象和数据结构都存储在私有堆空间中。程序员没有访问堆的权限，只有解释器才能操作。

例如Python万物皆对象，并且将内存操作封装的很好，所以python的基本数据类型所用的内存会要远大于存放纯数据类型所占的内存，例如，我们都知道存储int型数据需要四个字节，但是使用Python 申请一个对象来存放数据的话，所用空间要远大于四个字节。

C++内存管理 #

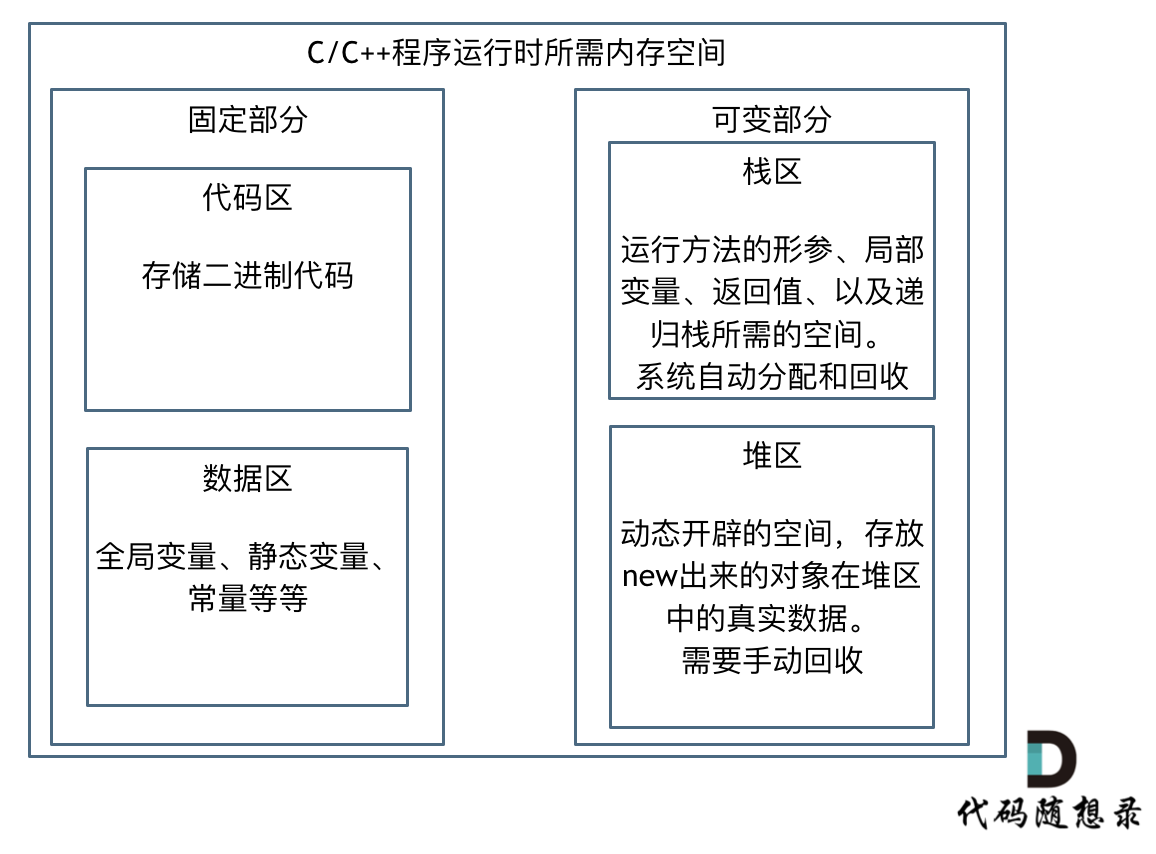代码区和数据区所占空间都是固定的，而且占用的空间非常小，那么看运行时消耗的内存主要看可变部分。

在可变部分中，栈区间的数据在代码块执行结束之后，系统会自动回收，而堆区间数据是需要程序员自己回收，所以也就是造成内存泄漏的发源地。

而Java、Python的话则不需要程序员去考虑内存泄漏的问题，虚拟机都做了这些事情。

内存对齐 #

不要以为只有C/C++才会有内存对齐，只要可以跨平台的编程语言都需要做内存对齐，Java、Python都是一样的。

这是面试中面试官非常喜欢问到的问题，就是：为什么会有内存对齐？

主要是两个原因

1. 平台原因：不是所有的硬件平台都能访问任意内存地址上的任意数据，某些硬件平台只能在某些地址处取某些特定类型的数据，否则抛出硬件异常。为了同一个程序可以在多平台运行，需要内存对齐。
2. 硬件原因：经过内存对齐后，CPU访问内存的速度大大提升。

假设CPU把内存划分为4字节大小的块，要读取一个4字节大小的int型数据，来看一下这两种情况下CPU的工作量：

内存对齐的情况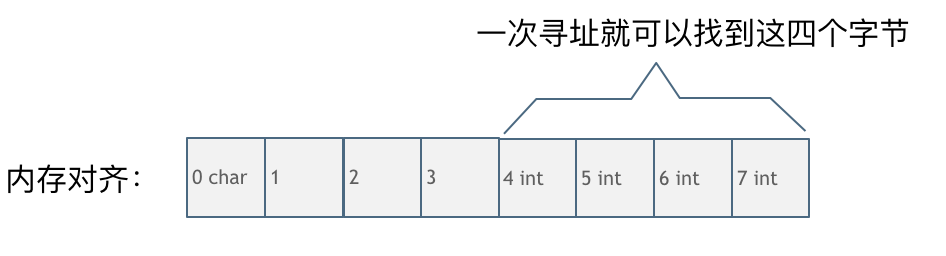： 一字节的char占用了四个字节，空了三个字节的内存地址，int数据从地址4开始。

此时，直接将地址4，5，6，7处的四个字节数据读取到即可。

内存没对齐的情况：

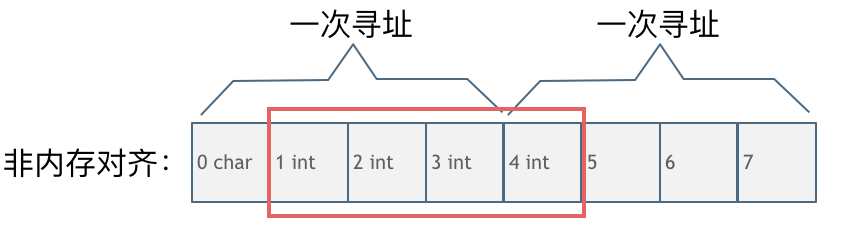char型的数据和int型的数据挨在一起，该int数据从地址1开始，那么CPU想要读这个数据的话来看看需要几步操作：

1. 因为CPU是四个字节四个字节来寻址，首先CPU读取0，1，2，3处的四个字节数据
2. CPU读取4，5，6，7处的四个字节数据
3. 合并地址1，2，3，4处四个字节的数据才是本次操作需要的int数据

此时一共需要两次寻址，一次合并的操作。

内存对齐岂不是浪费的内存资源么？

是这样的，但事实上，相对来说计算机内存资源一般都是充足的，我们更希望的是提高运行速度。

编译器一般都会做内存对齐的优化操作，也就是说当考虑程序真正占用的内存大小的时候，也需要认识到内存对齐的影响。